Monitores
Proyectores
Lámparas
Pantalla táctil interactiva | Signage
¿Cómo es un color “preciso”? ¿Cómo podemos cuantificar el color de una forma “precisa”? Antes de entrar en este tema, hablemos un poco más de por qué la cuantificación del color es importante para los fotógrafos, los diseñadores, los profesionales de la imagen, las personas que trabajan en el sector textil, etc.
Cuando intentamos describir un color, la forma más común de hacerlo es referirnos a un objeto de ese color. Por ejemplo, cuando describimos el color “rojo”, solemos utilizar la palabra “manzana” para describir el “rojo”. Pero, ¿de qué tipo de manzana hablamos? ¿Pensamos todos en la misma manzana? Observe la Figura 1: existen al menos siete tonos diferentes de “rojo” en las distantes variedades de manzana. Por no mencionar la última, que ni siquiera es roja. Por ello, se producen discrepancias cuando utilizamos objetos para describir colores. Debemos encontrar una forma de reducir las discrepancias al comunicarnos.

Figura 1: Diferentes variedades de manzana
Solemos utilizar “números” para expresar una medida precisa. Por ejemplo, utilizamos números para describir la longitud, el peso, etc. Por ello, necesitamos un modo de expresar los colores de forma numérica, para que podamos decir que el color A y el color B son iguales porque tienen los mismos valores numéricos. En 1913, la CIE (Comisión Internacional de la Iluminación) definió valores triestímulos (valores XYZ) para cuantificar los colores que podemos percibir los humanos. Los valores XYZ se obtienen multiplicando tres atributos (la distribución de energía espectral de la fuente de luz, la reflectividad del objeto y las funciones del observador estándar) para describir las características del sistema visual humano. El resultado es que, cuando el color A y el color B tienen los mismos valores XYZ, podemos afirmar que el color A y el color B son iguales.
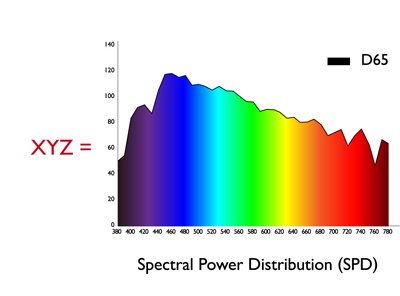
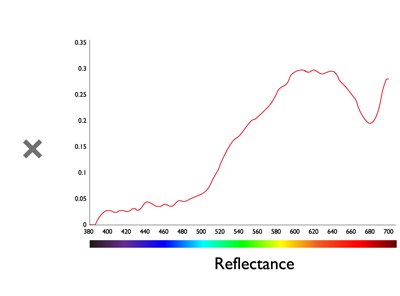
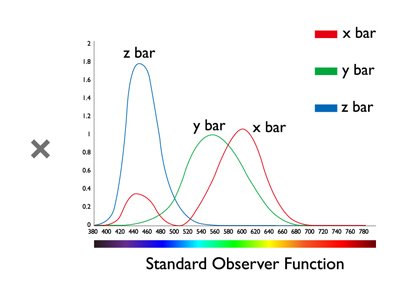
Figura 2: Fórmula para calcular los valores XYZ
Otra ventaja de definir los colores con valores numéricos es que podemos expresar fácilmente los colores en un diagrama con un sistema de coordenadas. Esto forma un espacio de color. En la Figura 3, se muestra el diagrama de cromaticidad xy de 1931 de la CIE, que representa todos los colores que podemos percibir. No obstante, este diagrama no refleja realmente la sensibilidad del sistema visual humano. Por ejemplo, pensemos en el azul y el verde. Los humanos somos muy sensibles al azul y menos sensibles al verde: con un poco más de rojo lo reconocemos como morado, y con un poco de verde lo reconocemos como cian. Este fenómeno no se refleja en la Figura 3, un diagrama de cromaticidad xy de 1931 de la CIE. Por ello, en 1976, se propuso el diagrama de cromaticidad con las coordenadas u’ y v’ para reflejar la sensación del sistema visual humano.
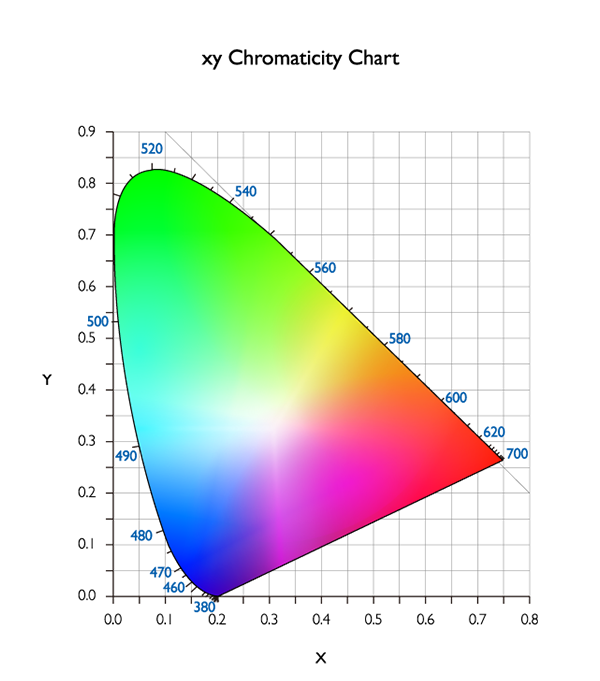
Figura 3: Diagrama de cromaticidad xy de 1931 de la CIE
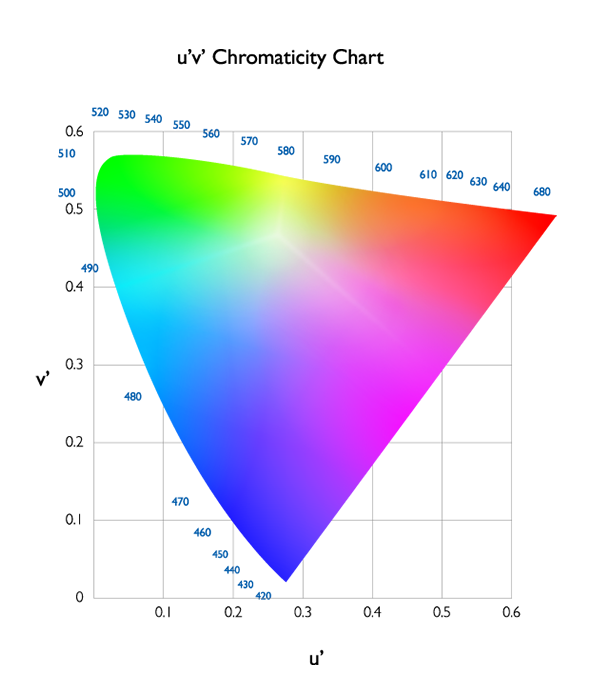
Figura 4: Diagrama de cromaticidad u’, v’ de 1976 de la CIE
Ya hemos definido un sistema para describir los colores de forma numérica.
Podemos utilizar una regla para medir la longitud y una balanza para medir el peso. Cuando medimos los colores, tenemos que medir antes la luz. Medir la luz no es tan fácil como utilizar una regla o una balanza, pero existen instrumentos que nos pueden ayudar. Por ejemplo, podríamos utilizar un espectrorradiómetro para medir la distribución de energía espectral de la luz.
Sin embargo, estos instrumentos son voluminosos y caros, y no es fácil llevarlos encima. Por ello, se ha desarrollado un dispositivo más simplificado llamado “colorímetro”. Un colorímetro mide la luz a través de un conjunto de filtros XYZ, por lo que es más rápido que el espectrorradiómetro, aunque menos preciso.
*Filtros XYZ: filtros ópticos que imitan las características ópticas de los valores XYZ (valores triestímulos) en cuando a transmitancia por longitud de onda.
Como dijimos anteriormente, cuando tenemos un conjunto de valores XYZ con los mismos números, podemos afirmar que estos colores son iguales. Sin embargo, en ocasiones los valores XYZ no son los mismos, pero siguen teniendo un aspecto muy similar. Por ejemplo, cuando vemos una luz clara en una habitación bien iluminada y una luz más tenue en una habitación sombría, los valores XYZ medidos no son los mismos (debido a la diferencia de intensidad de la luz), pero percibimos el mismo color de luz. Esto se debe a la adaptación de nuestro sistema visual. Vemos otro caso similar al comparar los colores de diferentes soportes. Por ejemplo, uno de un monitor y otro de un papel impreso. Por lo tanto, necesitamos otra métrica para cuantificar este fenómeno de adaptación. El espacio de color L*a*b* (que se muestra en la Figura 5), se propuso y se creó con este fin de “normalización”. Define el nivel de luz más brillante en una escena o un soporte (por ejemplo, el papel) como 100, y normaliza todos los demás colores de la escena o el soporte de acuerdo con la luz más brillante. Gracias a eso, ahora podemos comparar luces de diferentes intensidades o colores de diferentes soportes.
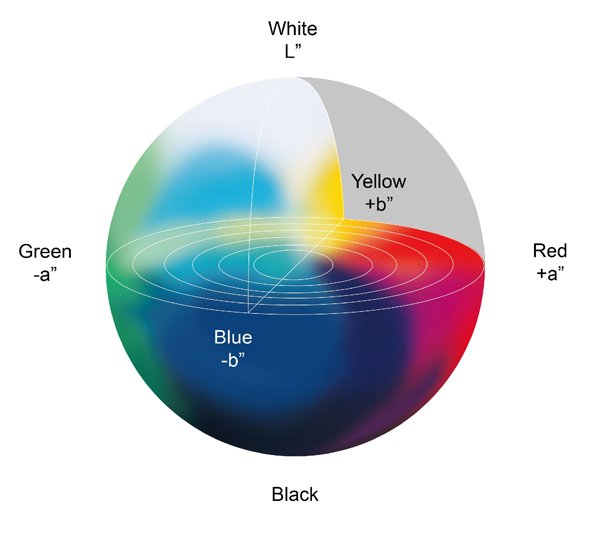
Figura 5: Espacio de color L*a*b*
As stated earlier, when we have a set of XYZ values with the same numbers, we could say these colors look the same. But there are occasions when the XYZ values are not the same, but they still look very similar. For example, when we see a bright light in a bright room versus a dimmer light in a dim room, the measured XYZ values are not the same (due to different light intensities, but we still perceive the same color of light. This is due to the adaptation of our visual system. Another scenario is to compare the colors from different media. For example, one from the monitor and one from the printed paper. Hence, we need another metric to quantify this adaptation phenomenon. L*a*b* color space (shown in Figure 5) was then proposed and built for this ‘normalization’ purpose. It defines the brightest level of light in a scene or a media (e.g. paper) as 100, and normalizes all other colors in the scene or media according to the brightest light. As a result, now we can compare light with different intensities or colors from different media.

Figure 5: L*a*b* Color Space
Cuando miramos dos colores similares, pero ligeramente diferentes, nos preguntamos cuánto se parecen. Sin utilizar valores numéricos para representar los colores, podríamos decir que “se parecen”. Pero, ¿cuánto? Y, si la percepción de los colores varía de una persona a otra, ¿cuál es la definición de “parecerse”? Con el espacio de color XYZ o el espacio de color L*a*b*, podemos cuantificar la diferencia existente entre colores. Calculando la distancia existente entre dos colores en un espacio de color específico (se suele utilizar el espacio de color L*a*b*), se puede obtener el valor de la diferencia. Este valor de la diferencia se llama “diferencia de colores”. Normalmente, utilizamos Delta E* para designar la “diferencia de colores”.
When we look at two similar, but slightly different colors, we will wonder how close these colors are? Without using numeric values to represent colors, we could say “it’s close”. But how close? And what is the definition of ‘close’ since the perception of colors vary from person to person. With the XYZ color space or L*a*b* color space, we can quantify the difference between colors. By calculating the distance between two colors in a particular color space (L*a*b* color space is usually used), a difference value can be obtained. This difference value is called ‘Color Difference’. We usually use delta E* for designating ‘Color Difference’.
La versión más simple de la fórmula de la diferencia de colores se llama Delta E* 76 (Delta E* ab).
En los sectores textil y de las artes gráficas se utiliza una fórmula más compleja. Se publicó en 1994, por lo que recibe el nombre de Delta E* 94.
En 2000, los investigadores desarrollaron una versión más reciente de la fórmula de la diferencia de colores para reflejar realmente lo que percibe el sistema visual humano. Se llama Delta E* 2000 (Delta E* 00). Gracias a la gran cantidad de estudios de investigación realizados para conseguir una elevada correlación entre los valores calculados y la percepción humana, la fórmula Delta E* 00 se ha convertido en estándar internacional y se recomienda su utilización en todos los trabajos de investigación científica.
Como hemos observado en las fórmulas anteriores, se necesitan dos conjuntos de valores L*a*b*. Si tenemos que determinar la precisión de un color específico, necesitamos un conjunto de valores L*a*b* medidos y un conjunto de valores L*a*b* definidos. Podemos obtener los valores medidos utilizando los instrumentos mencionados anteriormente, pero ¿cómo obtenemos los valores “definidos” o “estándar”? Podemos obtener los valores “definidos” o “estándar” utilizando gráficos estándar (Figura 6). Mediante estos gráficos de colores, se han definido los valores L*a*b* para todos los colores del gráfico, y cada gráfico se ha confeccionado poniendo mucho cuidado para cumplir la tolerancia. Por lo tanto, estos gráficos pueden utilizarse como referencia, pues los valores no cambiarán.
Para determinar la precisión de un color, suele utilizarse la fórmula Delta E* 00. Si Delta E* 00 < 1,00, significa que no existe diferencia perceptible para los expertos al comparar dos colores uno al lado del otro. Si Delta E* 00 < 3,00, significa que no existe diferencia significativa para una persona típica. (Con “expertos”, nos referimos a profesionales de la ciencia de los colores o fotógrafos, diseñadores, profesionales de la imagen, etc. con experiencia.)
En resumen, sabemos cómo utilizar los números para definir los colores y el motivo para hacerlo así. También hemos identificado las diferencias existentes entre los distintos espacios de color, como XYZ o L*a*b*. Y, por último, hemos aprendido formas de medir el color y cómo definir las diferencias entre los colores. Mediante valores basados en la fórmula Delta E* 00, podemos determinar si un color es preciso o no.

Figure 6-1: X-rite Classic ColorChecker Chart

Figure 6-2: X-rite Digital ColorChecker SG Chart

Figura 6-1: Gráfico de Classic ColorChecker de X-Rite

Figura 6-2: Gráfico de Digital ColorChecker SG de X-Rite